Higher-dimensional forcing -------------------- Bernhard Irrgang

personal homepage

university homepage

3 D forcing

young set theory

photos

Morasses

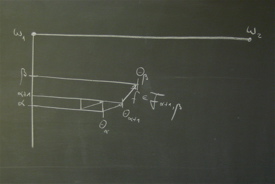
A simplified (κ,1)-morass is a structure M =<< θ_α | α ≤ κ >,< F_αβ | α < β ≤ κ >> satisfying the following conditions:
(P0) (a) θ₀ = 1, θ_κ = κ⁺, ∀α < κ  0 < θ_α < κ.
(b) F_αβ is a set of order-preserving functions f : θ_α → θ_β.
(P1) |F_αβ| < κ for all α < β < κ.
(P2) If α < β < γ, then F_αγ = {f ∘ g | f F_βγ,g F_αβ}.
(P3) If α < κ, then F_α,α+1 = {id ↾ θ_α,f_α} where f_α is such that f_α ↾ δ = id ↾ δ and f_α(δ) ≥ θ_α for some δ < θ_α.
(P4) If α ≤ κ is a limit ordinal, β₁,β₂ < α and f₁ F_β1α, f₂ F_β2α, then there are a β₁,β₂ < γ < α, g F_γα and h₁ F_β1γ, h₂ F_β2γ such that f₁ = g ∘ h₁ and f₂ = g ∘ h₂.
(P5) For all α > 0, θ_α = ⋃ {f[θ_β] | β < α,f F_βα}.

Lemma
Let α < β < κ, τ₁,τ₂ < θ_α, f₁,f₂ F_αβ and f₁(τ₁) = f₂(τ₂). Then τ₁ = τ₂ and f₁ ↾ τ₁ = f₂ ↾ τ₂.

A simplified morass defines a tree < T,≺>.
Let T = {< α,ν >| α ≤ κ,ν < θ_α}.
For t =< α,ν > T set α(t) = α and ν(t) = ν.
Let < α,ν >≺< β,τ > iff α < β and f(ν) = τ for some f F_αβ.
If s ≺ t, then f ↾ (ν(s) + 1) is uniquely determined by the lemma. So we may define π_st := f ↾ (ν(s) + 1).

Lemma
The following hold:
(a) ≺ is a tree, ht_T (t) = α(t).
(b) If t₀ ≺ t₁ ≺ t₂, then π_t0t1 = π_t1t2 ∘ π_t0t1.
(c) Let s ≺ t and π = π_st. If π(ν^′) = τ^′, s^′ =< α(s),ν^′ > and t^′ =< α(t),τ^′ >, then s^′≺ t^′ and π_s^′t^′ = π ↾ (ν^′ + 1).
(d) Let γ ≤ κ, γ Lim. Let t T_γ. Then ν(t) + 1 = ⋃ {rng(π_st) | s ≺ t}.

Example

As example, we force ω₂ ⁄→ (ω : 2)_ω² .
More precisely, we want to add a function f : [ω₂]² → ω such that {ξ < α | f(ξ,α) = f(ξ,β)} is finite for all α < β < ω₂.
For a,b ⊆ ω₂ set [a,b] := {< α,β >| α a, β b, β < α}.
Let P := {p : [a_p,b_p] → ω | a_p,b_p ⊆ ω₂ finite }.
We set p ≤ q iff q ⊆ p and ∀α < β a_q ∀ξ (b_p - b_q) ∩ α p(α,ξ)≠p(β,ξ).
Let π : λ → θ be an order-preserving map. Then π : λ → θ induces maps π : λ² → θ² and π : λ² × ω → θ² × ω in the obvious way:
π : λ² → θ², < γ,δ > < π(γ),π(δ) >
π : λ² × ω → θ² × ω, < x,ε > < π(x),ε > .

Base Case: β = 0
Then we only need to define P(1).
Let P(1) := {p P | a_p,b_p ⊆ 1}.

Successor Case: β = α + 1
We first define P(φ_β). Let it be the set of all p P such that
(1) a_p,b_p ⊆ φ_β
(2) f_α^-1[p], (id ↾ φ_α)^-1[p] P(φ_α)
(3) p ↾ ((φ_β \ φ_α) × (φ_α \ δ)) is injective
where f_α and δ are like in (P3) in the definition of a simplified gap-1 morass.
For all ν ≤ φ_α P(ν) is already defined. For φ_α < ν ≤ φ_β set P(ν) = {p P(φ_β) | a_p,b_p ⊆ ν}. Set σ_st : P(ν(s) + 1) → P(ν(t) + 1),pπ_st[p].

Limit Case: β Lim
For t T_β set P(ν(t) + 1) = ⋃ {σ_st[P(ν(s) + 1)] | s ≺ t} and P(λ) = ⋃ {P(η) | η < λ} for λ Lim where σ_st : P(ν(s) + 1) → P(ν(t) + 1),pπ_st[p].

Motivation

Two-dimensional applications

Three-dimensional application

Open problems